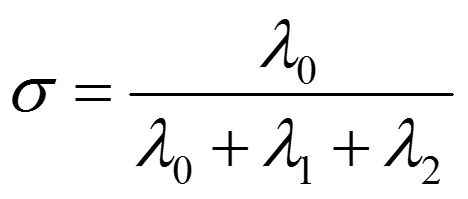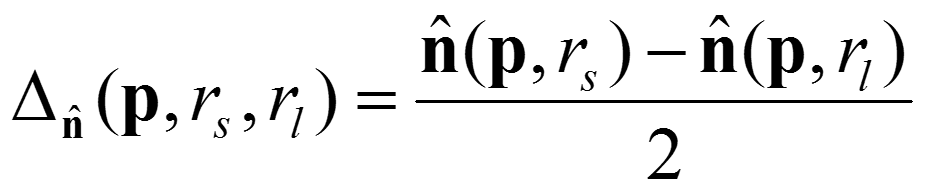※アクセス制限あり

[Japanese/English]

Combination of Curvatures and Difference of Normals (CCDoN)

Last updated： February 14, 2015.

　　　【参考文献】 　　　
  1. Y. Ioannou, B. Taati, R. Harrap and M. Greenspan, “Difference of Normals as a Multi-Scale Operator in Unorganized Point Clouds”, International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission (3DIMPVT), pp.501-508, 2012.
    2. 　　　
  2. 永瀬誠信, 秋月秀一, 橋本学 “CCDoN: ばら積み部品の高速・高信頼な6自由度位置姿勢推定のための局所特徴量”, 精密工学会誌, Vol.80, No.12, pp.1138-1143, 2014.
    3. 　　

  1. 概要
    2. 　Combination of Curvatures and Difference of Normals (CCDoN)は，ばら積み部品認識のための局所特徴量です． 注目点周りの複数の点群の情報を利用し，低次元で特徴量記述するため，高信頼かつ高速な照合が可能です．

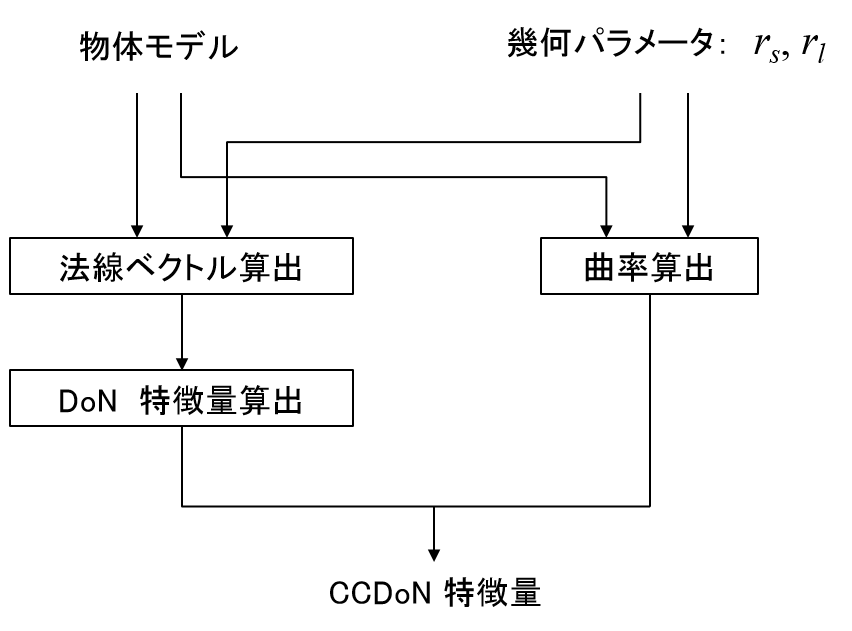
  2. アルゴリズムの流れ
    3. 　まず，3次元点群から構成される物体モデルと2つの球領域の範囲を設定する幾何パラメータ rs , rl を入力します． 次に，各特徴点の法線ベクトルを計算し，Ioannouらによって提案されたDifference of Normals (DoN)特徴量を記述します． また，設定した2つの球領域内のそれぞれの点群の分布をもとに注目点の曲率値を算出します． 最後に，DoN特徴量，2つの曲率値を統合することによってCCDoN特徴量を記述します．



  3. 法線ベクトルの算出
    4. 　注目点周辺の3次元点群を用いて共分散行列 C を作成し，固有値 λ0 , λ1 , λ2 (ただし，λ0 <= λ1 <= λ2) を算出します．


    pi は3次元点，p はpi の平均値を示します． C の最小固有値 λ0 の固有ベクトルが法線ベクトルとなります．

  4. 曲率の算出
    5. 　曲率は法線ベクトル算出時に用いた共分散行列 C の固有値 λ0 , λ1 , λ2 を用いて，以下の式によって算出します． 　曲率 σ は0から1までの値で算出されます．

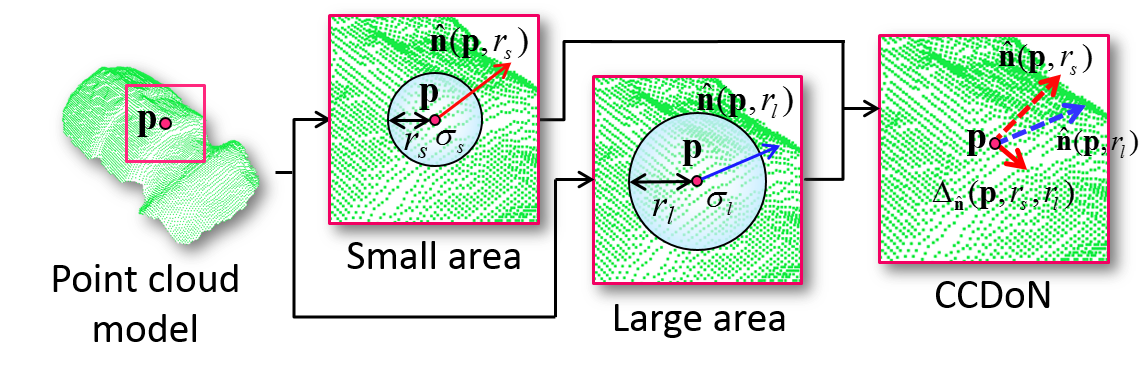
  5. DoN特徴量の記述
    6. 　まず，各点群に対して2つの異なる半径( rs < rl )の球領域を設定します． そして，2つの単位法線ベクトル n(p, rs ), n(p, rl )を算出し，これらを用いてDoN特徴量を算出します．


    DoN 特徴量は2 つの法線間の差分ベクトルであり，ノルムを計算することによって0 から1 までの値で算出されます．

  6. CCDoN特徴量の記述
    7. CCDoN特徴量は2つの異なる領域で算出した曲率値とDoN特徴量から構成されます．



    　 半径rs , rl の 曲率値σs ,σl を算出し，DoN特徴量と組み合わせることによって，CCDoN特徴量 F(||Δn || , σs , σl )を生成します． CCDoN 特徴量の各値は，法線間の差分値，特徴点周りの局所形状，大域形状を表現しています． 従来のDoN特徴量は特徴量を法線ベクトル間の差分で表現した相対的な値のみで記述するため，同じ相対値をもつ特徴点との誤照合をおこす可能性がありました． しかし，CCDoN特徴量はDoN特徴量に2つの曲率値を組み合わせているため，特徴量の信頼性が高まり，誤照合の低減が可能となります．さらに誤照合の低減によって，高速な照合も可能となります．
このページの制作：　橋本研究室（永瀬誠信）　Copyright 2015 ISL, Chukyo University

▲Topへ